Compressed sensing
Compressed sensing, also known as compressive sensing, compressive sampling and sparse sampling, is a technique for finding sparse solutions to underdetermined linear systems. In electrical engineering, particularly in signal processing, compressed sensing is the process of acquiring and reconstructing a signal that is supposed to be sparse or compressible.
Contents |
History
Several scientific fields used L1 techniques.[1] In statistics, the least-squares method was complemented by the 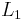 -norm , which was introduced by Laplace. Following the introduction of linear programming and Dantzig's simplex algorithm, the L1-norm was used in computational statistics. In statistical theory, the L1-norm was used by George W. Brown and later writers on median-unbiased estimators. It was used by Peter Huber and others working on robust statistics. The
-norm , which was introduced by Laplace. Following the introduction of linear programming and Dantzig's simplex algorithm, the L1-norm was used in computational statistics. In statistical theory, the L1-norm was used by George W. Brown and later writers on median-unbiased estimators. It was used by Peter Huber and others working on robust statistics. The 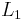 norm was also used in signal processing, for example, in the 1970s, when seismologists constructed images of reflective layers within the earth based on data that did not seem to satisfy the Nyquist–Shannon criterion.[2] It was used in matching pursuit in 1993, the LASSO estimator by Robert Tibshirani in 1996[3] and Basis Pursuit in 1998.[4] There were theoretical results describing when these algorithms recovered sparse solutions, but the required type and number of measurements were sub-optimal and subsequently greatly improved by compressed sensing. Around 2004 Emmanuel Candès, Terence Tao and David Donoho discovered important results on the minimum number of data needed to reconstruct an image even though the number of data would be deemed insufficient by the Nyquist–Shannon criterion.[5][6]
norm was also used in signal processing, for example, in the 1970s, when seismologists constructed images of reflective layers within the earth based on data that did not seem to satisfy the Nyquist–Shannon criterion.[2] It was used in matching pursuit in 1993, the LASSO estimator by Robert Tibshirani in 1996[3] and Basis Pursuit in 1998.[4] There were theoretical results describing when these algorithms recovered sparse solutions, but the required type and number of measurements were sub-optimal and subsequently greatly improved by compressed sensing. Around 2004 Emmanuel Candès, Terence Tao and David Donoho discovered important results on the minimum number of data needed to reconstruct an image even though the number of data would be deemed insufficient by the Nyquist–Shannon criterion.[5][6]
Underdetermined linear system
An underdetermined system of linear equations has more unknowns than equations and generally has an infinite number of solutions. However, if there is a unique sparse solution to the underdetermined system, then the Compressed Sensing framework allows the recovery of that solution. Not all underdetermined systems of linear equations have a sparse solution.
Solution / reconstruction method
Compressed sensing takes advantage of the redundancy in many of interesting signals—they are not pure noise. In particular, many signals are sparse, that is, they contain many coefficients close to or equal to zero, when represented in some domain.[7] This is the same insight used in many forms of lossy compression.
Compressed sensing typically starts with taking a weighted linear combination of samples also called compressive measurements in a basis different from the basis in which the signal is known to be sparse. The results found[6] by David Donoho, Emmanuel Candès, Justin Romberg and Terence Tao showed that the number of these compressive measurements can be small and still contain nearly all the useful information. Therefore, the task of converting the image back into the intended domain involves solving an underdetermined matrix equation since the number of compressive measurements taken is smaller than the number of pixels in the full image. However, adding the constraint that the initial signal is sparse enables one to solve this underdetermined system of linear equations.
The least-squares solution to such problems is to minimize the 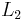 norm—that is, minimize the amount of energy in the system. This is usually simple mathematically (involving only a matrix multiplication by the pseudo-inverse of the basis sampled in). However, this leads to poor results for many practical applications, for which the unknown coefficients have nonzero energy.
norm—that is, minimize the amount of energy in the system. This is usually simple mathematically (involving only a matrix multiplication by the pseudo-inverse of the basis sampled in). However, this leads to poor results for many practical applications, for which the unknown coefficients have nonzero energy.
To enforce the sparsity constraint when solving for the underdetermined system of linear equations, one can minimize the number of nonzero components of the solution.
The function counting the number of non-zero components of a vector was called the 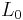 "norm" by David Donoho. The quotation marks served two warnings. First, the number-of-nonzeros
"norm" by David Donoho. The quotation marks served two warnings. First, the number-of-nonzeros 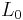 -"norm" is not a proper F-norm, because it is not continuous in its scalar argument: nnzs(αx) is constant as α approaches zero. Unfortunately, later authors have neglected Donoho's quotation marks and abused terminology—clashing with the established use of the
-"norm" is not a proper F-norm, because it is not continuous in its scalar argument: nnzs(αx) is constant as α approaches zero. Unfortunately, later authors have neglected Donoho's quotation marks and abused terminology—clashing with the established use of the 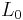 norm for the space of measurable functions (equipped with an appropriate metric) or for the space of sequences with F–norm
norm for the space of measurable functions (equipped with an appropriate metric) or for the space of sequences with F–norm 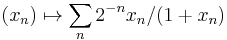 . [8]
. [8]
Candès. et. al., proved that for many problems it is probable that the 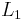 norm is equivalent to the
norm is equivalent to the 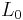 norm, in a technical sense: This equivalence result allows one to solve the L1 problem, which is easier than the
norm, in a technical sense: This equivalence result allows one to solve the L1 problem, which is easier than the 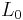 problem. Finding the candidate with the smallest
problem. Finding the candidate with the smallest 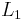 norm can be expressed relatively easily as a linear program, for which efficient solution methods already exist.[9] When measurements may contain a finite amount of noise, basis pursuit denoising is preferred over linear programming, since it preserves sparsity in the face of noise and can be solved faster than an exact linear program.
norm can be expressed relatively easily as a linear program, for which efficient solution methods already exist.[9] When measurements may contain a finite amount of noise, basis pursuit denoising is preferred over linear programming, since it preserves sparsity in the face of noise and can be solved faster than an exact linear program.
Implementations
The field of compressive sensing is related to other topics in signal processing and computational mathematics, such as to underdetermined linear-systems, group testing, heavy hitters, sparse coding, multiplexing, sparse sampling, and finite rate of innovation. Imaging techniques having a strong affinity with compressive sensing include coded aperture and computational photography.
Starting with the single-pixel camera[10] from Rice University, an up-to-date list of the most recent implementations of compressive sensing in hardware at different technology readiness level is available.[11] Some hardware implementation (like the one used in MRI or compressed genotyping) do not require an actual physical change, whereas other hardware require substantial re-engineering to perform this new type of sampling. Similarly, a number of hardware implementations already existed before 2004; however, while they were acquiring signals in a compressed manner, they generally did not use compressive sensing reconstruction techniques to reconstruct the original signal. The result of these reconstruction were suboptimal and have been greatly enhanced thanks to compressive sensing.
Compressive sensing in the news
Compressed sensing was in the news as part of the single-pixel camera[10] from Rice University. Some aspects of compressed sensing were featured in Wired's "Engineers Test Highly Accurate Face Recognition".[12] A more recent article in Wired described compressed sensing as a full-fledged technique in "Using Math to Turn Lo-Res Datasets Into Hi-Res Samples".[13] Because the article was talking about sampling for MRI, some confusion might have occurred.[14][15]
See also
References
- ^ List of L1 regularization ideas from Vivek Goyal, Alyson Fletcher, Sundeep Rangan, The Optimistic Bayesian: Replica Method Analysis of Compressed Sensing
- ^ Hayes, Brian, The Best Bits, American Scientist, July 2009
- ^ The Lasso page, at Robert Tibshirani's homepage. "Regression shrinkage and selection via the lasso". J. Royal. Statist. Soc B., Vol. 58, No. 1, pages 267-288
- ^ "Atomic decomposition by basis pursuit", by Scott Shaobing Chen, David L. Donoho, Michael, A. Saunders. SIAM Journal on Scientific Computing
- ^ E. J. Candès, J. Romberg and T. Tao. Stable signal recovery from incomplete and inaccurate measurements. Comm. Pure Appl. Math., 59 1207-1223 [1]
- ^ a b Donoho, D. L., Compressed Sensing, IEEE Transactions on Information Theory, V. 52(4), 1289–1306, 2006 [2]
- ^ Candès, E.J., & Wakin, M.B., An Introduction To Compressive Sampling, IEEE Signal Processing Magazine, V.21, March 2008 [3]
- ^ Stefan Rolewicz. Metric Linear Spaces.
- ^ L1-MAGIC is a collection of MATLAB routines [4]
- ^ a b http://dsp.rice.edu/cscamera
- ^ Compressive Sensing Hardware, http://sites.google.com/site/igorcarron2/compressedsensinghardware
- ^ Engineers Test Highly Accurate Face Recognition
- ^ http://www.wired.com/magazine/2010/02/ff_algorithm/all/1
- ^ Why Compressed Sensing is NOT a CSI "Enhance" technology ... yet !
- ^ Surely You Must Be Joking Mr. Screenwriter
Further reading
- Using Math to Turn Lo-Res Datasets Into Hi-Res Samples Wired Magazine article
- Compressive Sensing Resources at Rice University.
- Compressed Sensing: The Big Picture
- A list of different hardware implementation of Compressive Sensing
- Compressed Sensing 2.0
- Compressed Sensing Makes Every Pixel Count – article in the AMS What's Happening in the Mathematical Sciences series
- Nuit Blanche A blog on Compressive Sensing featuring the most recent information on the subject (preprints, presentations, Q/As)
- Online Talks focused on Compressive Sensing